The Impossible Man: Roger Penrose and the Cost of Genius Patchen Barss Basic (2024)
In the early days of a book project that would span six years, writer Patchen Barss had the best stroke of luck a biographer can hope for. His subject, the Nobel prizewinning mathematical physicist Roger Penrose, brought him a bundle of hundreds of letters that he had written decades earlier to a friend and confidante, a mathematician called Judith Daniels. After Daniels died of cancer in 2005, her sister found and returned the letters. Expecting them to contain insights into the development of his ideas in the 1970s, Penrose had decided to share them in full.
As Barss relates in The Impossible Man, Penrose had not even looked at the letters again before opening the package in front of his biographer. He started reading, and tears began to roll down his face, as the letters revealed much more than his inner processes of working. The episode goes a long way towards explaining the extraordinary access Barss got into Penrose’s private life — and into details that Penrose had perhaps buried deep in his memory.
Does quantum theory imply the entire Universe is preordained?
The Impossible Man is the first book-length biography of Penrose, a demi-god of mathematical physics and one of the few survivors among the pioneers who established the theory of black holes. Although Barss is more at home detailing the personal aspects of Penrose’s life than describing his science, he offers more than a glimpse of Penrose’s intellect.
The book portrays the mathematician as in equal parts hugely influential and endlessly contentious, and as a man whose visual imagination and artistry helped him to discover patterns of eternal beauty1. The book is also a meditation on the human costs of being a person of genius and how others often bear those costs.
Penrose was born in 1931 in Colchester, UK, into a family of intellectual overachievers. The book describes how his father, geneticist Lionel Penrose, was emotionally distant and bonded with his four children only over intellectual pursuits such as chess, games of logic or calculus. Lionel exerted suffocating control over his wife, Margaret, a trained physician whom he prevented from practising, and who retreated into isolation. Barss describes how the emotional neglect Penrose experienced from both parents was later mirrored in his relationships with his own children, and might have doomed his first marriage, to the US-born Joan Wedge, from the beginning.
Original thinker
The young Penrose displayed an early, prodigious affinity for geometric patterns. Against the wishes of his father, who wanted Roger to study medicine and saw professional mathematicians as “peculiar, unworldly people”, he decided to study mathematics. Initially, he concentrated on pure, unadulterated theoretical topics. However, during his degree studies at University College London and the University of Cambridge, UK, in the early 1950s, he also developed an interest in Albert Einstein’s general theory of relativity and in quantum physics, after attending classes by another Nobel prizewinner, Paul Dirac.
Penrose’s superpower throughout his career has been an ability to leverage his geometric intuition into physical insights that others have missed. Most mathematicians and physicists will have come across a concept of his making, from the Penrose diagrams, which provide a graphic representation of the past, present and future of a universe, to the ‘tensor networks’ that have become a foundational tool in machine learning.
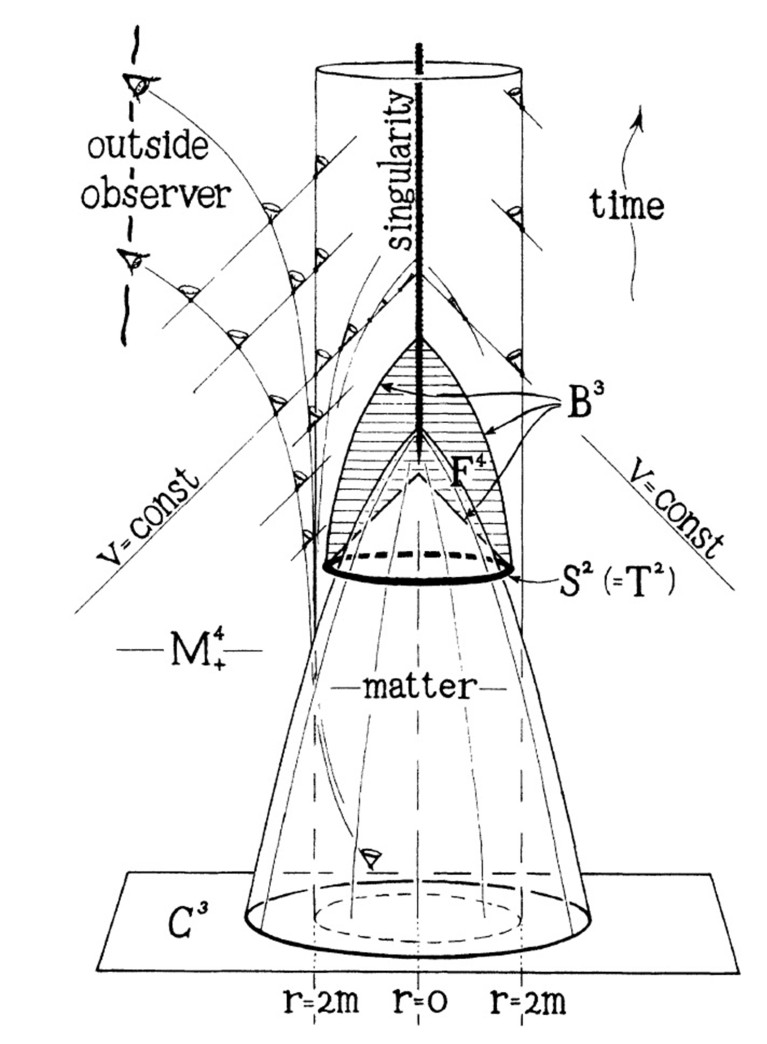
In a 1965 paper, Roger Penrose proved that inside a black hole, space-time must collapse into a ‘singularity’ where time itself ends.Credit: R. Penrose/PRL
A central theme in Penrose’s work — since an epiphany during a road trip in Texas in 1963 — has been the development of the theory of ‘twistors’. In this, Penrose was motivated, in part, by his love of complex numbers, which are needed to solve otherwise impossible equations such as x2 = –1. The algebra of complex numbers finds its most natural expression in the pleasingly symmetrical geometry of curves on a sphere. Penrose’s twistors attach a deeper meaning to them, by reinterpreting every point of space-time as a complex sphere.
Penrose and his school of ‘Twistorians’ hope that this concept will ultimately allow them to reconcile gravity with quantum physics. That goal might still be far away, but some of the mathematical ideas are slowly becoming part of theoretical physicists’ toolkit.
On the fringes
Barss recounts with increasing frustration how Penrose also began to put a lot of his energies into the pursuit of ideas that most other researchers either ignored or derided. That dualism between canon and heresy is epitomized by Penrose’s Nobel lecture in 2020.

